Crypto Series: Differential Fault Analysis by examples
So, after more than a year without writing anything here, I was bored today and thought it would be nice to share a new piece on attacking cryptographic implementations here 🙂
Differential Fault Analysis (DFA) attacks are part of what is known as fault injection attacks. This is, they are based on forcing a cryptographic implementation to compute incorrect results and attempt to take advantage from them. With fault injection attacks (also often called active side channel attacks) one can achieve things like unauthenticated access to sensitive functionality, bypassing secure boot implementations, and basically bypassing any security checks an implementation performs.
With DFA attacks, one is able to retrieve cryptographic keys by analyzing correct/faulty output pairs and comparing them. Of course, this assumes you are able to inject faults somehow... which is often true in hardware implementations: gaming consoles, STBs, smart cards, etc. At the software level, one can achieve similar things by debugging the implementation and changing data or by patching instructions... but this is something we have been doing for a long time, haven't we? 🙂 I often say that fault injection attacks are the analog version of 'nopping' instructions out in a program, although we often do not know exactly what kind of faults we are injecting (i.e. we often miss a fault model, but we still successfully attack implementations in this way).
There are ways to protect against this kind of attack as an application programmer, but this is not the objective of this post. In the remainder of this post, I will explain two powerful DFA attacks on two modern cryptographic algorithms: RSA and (T)DES. For some information on protecting from these attacks as a programmer, take a look at these slides. If there is some interest, I will outline the most common techniques to perform fault attacks in a future post.
Crypto-series: Elliptic Curve Cryptography
After a long long while, it's time to go on with our crypto series. Last time we talked about the RSA cryptosystem, and we learned its security is based on the integer factorization problem (plus the DL problem for message secrecy). Today, we'll continue with public key cryptosystems: we'll look into Elliptic Curve Cryptography.
Elliptic Curves
If we are talking about Elliptic Curve Cryptography, first we need to define what an Elliptic Curve is. Mathematically, an Elliptic Curve is a curve with the following equation:
This means that every point (x,y) for which the above expression is met will be part of the curve. However, it turns out in our case we can simplify the equation because the curves we'll be using can generally be written as:
Such a curve, over the reals (i.e. x and y are real numbers) and with a=-3, b = 1, looks like this:
What makes these curves special is that we can define an abelian group with them. To do that, we define the point at infinity and an addition law. The addition law is depicted in the following picture from Wikipedia:
As you can see, if you want to add two points P and Q, you draw a line through them. The intersection of this line and the curve is the point -(P+Q). Then, you just need to invert this point (negate the y coordinate) to obtain the final result.
Of course, we have special cases. If the point is added to itself, the line is defined as the tangent to the curve at that point, as intuitively the tangent touches 'two times' the point.
If we add a point to its inverse, we get a vertical line... and that's a problem because it will never touch the curve. Here is where the point at infinity comes to rescue. The point at inversity is simply 'up there' (and 'down there'), and is the zero element of the group.
Elliptic Curves for Cryptography
We have defined above how an elliptic curve looks like over the reals, and how to perform additions of two points. Obviously, when addition is defined we also have multiplication for free: just add a point to itself several times in a row (although you can do it in smarter and more efficient ways).
But how do we use it for cryptography? I mean, where is the difficult problem here? Actually, the difficult problem is again the discrete logarithm problem. In this case, we define it as follows:
Given a curve E and all its parameters, a base point P and a point Q=nP, obtain n.
And how is this difficult in the curves defined above, you might be thinking... The truth is we do not use real curves in ECC, but we use curves over finite fields instead. We can do it over prime fields GF(p), or we can do it over binary fields GF(2^n). I'll look only at GF(p) here, but similar concepts apply (although the simplified expression I defined above is slightly different in that case).
So, the curve I depicted previously taken over GF(8761) looks like this:
Messy, huh? Exactly the same addition laws apply here, but now when you add two points you draw a line... and when the line gets out of the GF(p) x GF(p) plane it wraps around and comes back from the other side. It is a little more difficult to depict and to visualize, but the concept is the same as before. And now you probably start seeing why this is difficult to solve...
Why Elliptic Curves?
Now you might be wondering... why do we use Elliptic Curve cryptography at all? What are the benefits? The answer is that the ECC allows us to use smaller keys than other algorithms like RSA / 'normal' DL systems for the same amount of security.
This is because the best known general methods for solving the DL in Elliptic Curve are of exponential complexity, while for the other systems we know subexponential methods. Hence, the DL problem under Elliptic Curves is believed to be more difficult than the equivalent base problems for other public key cryptosystems.
Now that we know how elliptic curves are used in cryptography and what benefits they have over traditional
Elliptic Curve Diffie-Hellman
So, if you remember from when we talked about Diffie-Hellman, this is a key exchange protocol that relies on the Discrete Logarithm problem (and the Diffie-Hellman assumption). Usually this is done over a finite field GF(p), but now we have just defined a group based on Elliptic Curves which we can use as well.
In this case, Alice has a private key and a public key
, where G is the base point. Similarly, Bob has
and
. Alice and Bob exchange public keys, and then each of them can compute a common point
.
This protocol relies on the assumption that the DL problem is infeasible in the elliptic curve (which requires a base point G of high order) and the Diffie-Hellman assumption.
Other ECC algorithms
Besides the EC Diffie-Hellman algorithm defined above, there are several other algorithms based on Elliptic Curves. For example, one could compute digital signatures using Elliptic Curve DSA or Elliptic Curve Nyberg Rueppel. Each algorithm has its own details, but the important problem used as a foundation for each of them is the Discrete Logarithm problem over Elliptic Curves as we have defined it here.
Beware, however, that similarly to other algorithms, ECC algorithms rely also on other conditions. For example, for ECDSA (and DSA) there is a secret parameter that must be unique, and two signatures with the same value for this parameter will reveal your secret key. As usual, if you implement cryptography. you need to be aware of the requirements and limitations or you will certainly screw up (toc toc SONY!).
On Padding Oracles, CBC-R and timing attacks…
Somewhere before the weekend I was discussing about Padding Oracles with a friend and somehow it came up that there was no public tool using timing information for this kind of attacks.
I had seen that Thai and Juliano mentioned timing leaks in their talk at EkoParty, but since AFAIK there was no public tool available I decided to look into it. Also, some weeks ago I added the CBC-R encryption part to my scripts, in order to be able to encrypt arbitrary information as long as we are able to control the IV.
So in this post I'm going to write about these two things: CBC-R encryption and a web based padding oracle attack script using timing information.
Crypto Series: Mifare Crypto1
Let's go back into Cryptography. This time I'll tell you how the (in)famous Crypto1 cipher works. It is used in the Mifare Classic RFID tags, typically used for building access control but also for many other systems such as the Oyster Card in London, the OV-Chipkaar in The Netherlands, etc.
We won't talk about the protocol details, nor about how the published attacks work. You'll find a couple of interesting links at the end though ;-).
Note: Images obtained from the papers linked at the end of the post.
The Crypto1 cipher
Crypto1 is a proprietary stream chiper from NXP found in the RFID tags from the Mifare Classic family. At first, it was studied by Karsten Nohl reverse engineering the chip itself. This information was published in the CCC 07, although not many details about the cipher were published.
In parallel, the Radboud Universiteit from Nijmegen was studying this kind of cards and with the help of the information published at CCC completely reverse engineered the cipher and published the details. Let's see how it works then...
Linear Feedback Shift Registers (LFSRs)
In this post I'll provide a very simple description of linear feedback shift registers (LFSR for short). Further, we'll see how they are used to create stream ciphers. And all these things without going into mathematical details, for which I refer the interested reader to documents such as the Handbook of Applied Cryptography or this LFSR Reference.
Shift Registers
A shift register is basically a construction with interconnected several memory cells, where every cell stores one bit. So, the value of these cells conforms the so-called state of the register. When the register steps from one state to the next one (usually at each clock tick), the new state is created by simply shifting the bit in a cell to the cell next to it. Thus, the right-most bit goes out of the register, and a new bit goes into the left-most cell.
In this picture we can see an implementation of a 4 bit shift register:

Shift register
We can see an input line (Data in), 4 points where one can read the current state (Q1-Q4) and a clock input, which governs the register telling it in which moment it should step into the next state.
Linear Feedback Shift Registers (LFSRs)
Well, once you know what a shift register is, it is fairly straightforward to understand how a LFSR works. We just take the previous register and set the input as a linear combination of the different cells. Since there is a loop which feeds the register based on its previous state, we have feedback. Further, since this feedback is based on a linear function, then we have linear feedback, hence the name :).
LFSRs' use in cryptography
So far, you probably have guessed that the main use of an LFSR in encryption systems is generating a series of pseudo-random bits to be used as a key stream in a stream cipher.
The idea is to generate a stream of bits with the minimum repetition possible, i.e. with maximal period. For its study, the connections in an LFSR are usually represented as a polynomial and the properties such a polynomial needs to meet to achieve maximal period are analyzed.
Basically, we need to get the LFSR to run through all its possible states before going back into the first one. So, if we have 16 bit registers, we'd want to have the LFSR pass through the 2^16-1 states before cycling back to the first one. And yes, I said 2^16-1 instead of 2^16 because the zero state should never appear. Otherwise the LFSR will never leave this state, since the feedback function is linear. For the curious readers, an LFSR will have maximal period if its generating polynomial is a so-called primitive polynomial (I'm pretty sure this name will ring a bell for some of you guys, although maybe not as a happy memory :P).
Setting aside the study of these polynomials, which involves somewhat comlex maths (to my non-mathematician opinion 😆 ), an LFSR by itself should not be used as a key stream generator because its properties make it fairly predictable. In fact, given an n bit LFSR, obtaining 2n bits of its output it is possible to recover the generating polynomial and be able to decrypt any subsequent text.
Therefore, LFSRs are not directly used in crypto, but they are generally used in one of these modes:
- Nonlinear combination of LFSRs: the output from several LFSRs is combined in a non-linear fashion to obtain a key stream.
- Nonlinear filter generator: the output is generated from a non-linear combination of the state.
- Clock-controlled generators: In this mode, several LFSRs step based on some rules, instead of stepping for every clock cycle.
With this kind of constructions it is possible to improve LFSR's properties for the creation of secure stream ciphers. And that's it for LFSRs from my side, for more information refer to these references:
Handbook of Applied Cryptography
Crypto Series: Introduction to stream ciphers
Today we're gonna step a little further in our Crypto series. We'll see the main properties of the so-called Stream Ciphers, how they work and some things that should be taken into account when they are used.
Later in this series, we'll see how Linear Feedback Shift Registes (LFSR) work and we'll see one of the most used stream ciphers, together with an example of wrong usage.
Keep on reading to learn more about this class of ciphers.
Crypto Series: Block Ciphers – Data Encryption Standard (DES)
The Data Encryption Standard ( DES ) was designed by IBM in 1973 as a submit for a call for proposals by the National Bureau of Standards of the United States. There was some controversy regarding to the involvement of the NSA in the development of the cipher, especially to the mysterious S-boxes and the reduced key size used, but years later it was shown that the S-boxes used where more resistant to Differential Cryptanalysis than if they had been selected at random.
The algorithm was approved as a FIPS standard in 1976, and revised up to three times in 1988,1993 and 1999. The last revision FIPS-46-3 describes the 3DES extension as a method to enlarge the key size of the DES cipher by using 3 DES operations in a row, encrypting the first time, decrypting the second time, and encrypting again the third time. This was done in order to withstand an efficient brute force attack published in 1998.
After the break (click Read more!) we'll see how it works and the main components of the algorithm.
NOTE: All images in this post are directly linked to Wikipedia. If the images are not visible anymore, let me know in the comments and I'll post my own version of the images.
Crypto Series: Block ciphers
In this entry we introduce block ciphers in a general way, as well as its modes of operation. Further, we'll see how to generate message authentication codes (MAC) using block ciphers.
Block ciphers
As we already said in the previous entry, block ciphers are symmetric ciphers which encrypt fixed length blocks. Therefore, a block cipher generally applies a series of operations combining the input block and the secret key (which isn't necessarily the same length) to obtain the output block (ciphertext).
Since they are symmetric, the decryption primitive uses the same key as the encryption primitive, and applies the operations needed to get back the plaintext at its output:
Most block ciphers can be classified as product ciphers or iterative block ciphers, based on a series of basic operations (rounds) which are repeated a number of times. These rounds provide confusion and difusion to the cipher, two concepts identified by Shannon in his famous treaty about communication theory.
Confusion refers to breaking the relationship between ciphertext and key as much as possible, while diffusion refers to destroying the statistical characteristics of the message source. Shannon identified these concepts and established the need for a secure cipher to provide them.
These kind of ciphers are generally Substitution-Permutation Networks (SPN), where several permutations (scrambling) and substitutions (changing values for others) take place one after the other, using a key, trying to achieve the goal: destroy the statistical properties of the source and obtain a secure cipher.
In subsequent entries we'll see how DES and AES, two well-known symmetric encryption standards, work. The remaining of this article treats block cipher modes of operation and how to authenticate messages using these ciphers.
Crypto Series: Introduction to Cryptool
In this post we'll see some of the options provided by Cryptool to analyze classical ciphers, as well as using it for breaking a ciphertext encrypted with Vigenère's cryptosystem.
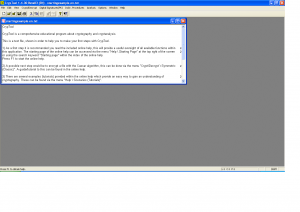
First step, as usual, consists of installing Cryptool. To that end, I chose using a virtual machine in VMWare with Windows XP. The installation is very simple, typical Windows app installation: Next, Next,... We'll use the English version, which is the one I have installed, but it shouldn't be difficult to follow our steps with a different version.
Once installed, this is how the main window of Cryptool looks like:
Looking at the menus, one can see that Cryptool offers (amongst others) the possibility to encrypt and decrypt texts, cryptanalytic tools and guided tutorials. In this text we'll see how to use Cryptool for analyzing encrypted texts... Let's start with an easy one:
Gznyrém xlmlxrwz xlnl Fmrevihrwzw Klorgéxmrxz wv Ezovmxrz, l vo
Klor kziz olh znrtlh, vh fm lhxfil oftzi oovml wv vhgfwrl b kvievihróm.
Hlyivglwl, klijfv glwl zjféo ol hfurxrvmgvnvmgv olxl xlnl kziz vmgizi
vm vooz, gvmwiá jfv szxvi zotl wv ol zmgvirlinvmgv xrgzwl kziz hzori
zrilhl wv vooz. Vmgiv olh oftzivh náh xlmxfiirwlh, hv vmxfvmgizm oz
Xzhz wvo Zofnml (szyrgfzonvmgv fhzwz kziz wlinri olh qfvevh wv
nzwiftzwz, kvil gznyrém kziz qftzi z yroozi l ufgyloím, zfmjfv mlh
jfrgzm vhgv vm éklxz wv vcánvmvh), oz Yryorlgvxz (wlmwv oz tvmgv hv
wrervigv vhgfwrzmwl), b ozh krhgzh wv gvmrh b káwvo.
The text has been obtained from IEEE's cryptography challenge, by Javi Moreno and Amine Tourisa (sorry, Spanish). Actually, the solution was already published in Javi's blog, but we're gonna see how to obtain it with Cryptool:
- Create a new document ( File | New )
- Copy the text from the challenge
- Go to Analysis | Tools for Analysis | Histogram
Now we get the following frequency diagram from the text:
Next we just compare this diagram with the typical one from Spanish or English, and we can see that it's simply been 'mirrored'... easy, isn't it? So the answer is, as you probably guessed, ATBASH. Decrypting the text with ATBASH (Crypt/Decrypt | Symmetric (Classic) | Substitution/Atbash ... ) , we get this cleartext (again, Spanish):
También conocida como Universidad Politécnica de Valencia, o el Poli para los amigos, es un oscuro lugar lleno de estudio y perversión. Sobretodo, porque todo aquél lo suficientemente loco como para entrar en ella, tendrá que hacer algo de lo anteriormente citado para salir airoso de ella. Entre los lugares más concurridos, se encuentran la Casa del Alumno (habitualmente usada para dormir los jueves de madrugada, pero también para jugar a billar o futbolín, aunque nos quitan este en época de exámenes), la Biblioteca (donde la gente se divierte estudiando), y las pistas de tenis y pádel.
Now we'll see how to solve a Vigenère encrypted text. Let's take as our working example the following text:
Crypto Series: WWII – Enigma
With this post we're leaving classical pencil and paper ciphers and getting into the mechanic ciphers used during the World War II era. We're gonna see the most famous of the cipher machins, the Enigma machine used by the Germans. Our analysis will be based on the book Applied Cryptanalysis from Mark Stamp and Richard M. Low. A very recommendable book if you are interested on cryptanalysis, really.
The Enigma Machine
The Enigma machine was developoed and patented by Arthur Scherbius in 1918, and was adopted by the nazi Germany for military and diplomacy use. Polish cryptanalysts broke the Enigma cipher in the late 1930s, and Allieds exploited this knowledge during WWII.

Máquina Enigma
It is said that thanks to Enigma being broken without the Germans noticing it (thanks to the more or less careful use of the obtained intelligence) the WWII was shortend one year or even more. There has been a lot of writing around Enigma, and I'm not an expert in the field, so I refer you to Google if you want more historical information 🙂
Encrypting and decrypting with Enigma
To encrypt with Enigma, after initializing the machine with the key as we'll see later, one simply had to press the plaintext letter to encrypt in the keyboard, and then the corresponding ciphertext letter would be enlightened in the upper (back-lighted) keyboard.
To decrypt, one had to set the machine into the corresponding state and press the received ciphertext letter. Then, in the upper keyboard the plaintext letter would get enlightened.
Enigma's features
Enigma was an electro-mechanical machine, based on the use of rotors. In the previous figure, one can easily see the mechanical keyboard and the back-lighted keyboard, which worked as input and output of the device.
Further, there is what seems to be a switchboard (stekker in German) with cables connecting one of the ends with another, and three rotors in the upper side of the machine. The configuration of these rotors and the cables of the stekker are the initial key of the machine.
Once the machine was initialized, it was possible to press in the keyboard the plaintext or ciphertext letters and obtain the ciphertext or the plaintext respectively. The workings of the machine were essantially as follows:
After pressing a key in the keyboard, a signal was sent through the corresponding stekker pin. Thanks to the cable configuration, this signal was transmitted to a different letter. Thus, the stekker worked as a mapping in the alphabet, where each letter was substituted by another one: a simple substitution.

Rotores de la máquina Enigma
After it, the signal went through the three rotors, reflected in the reflector and went back through the rotors (see figure). Finally, from the rotors it went again through the stekker, which performed a new substitution, and turned on the backlight of the corresponding letter. The net effect of the rotors and the reflector was again a permutation: each letter was converted into a different one.
However, if this were it, we would have no more than a simple substitution, with the only complexity of the use of an electromechanical machine. What Enigma added was a variation of the disposition of these rotors.
Each time a key was pressed, the rightmost rotor stepped one position. The middle rotor stepped in an odometer-like fashion, each time the rightmost rotor went through all of its steps. The leftmost rotor stepped in the same way, but depending on the middle rotor.
Further, it was possible to select the point where each rotor would step. This means that it could be when the previous rotor reached the initial position, but it could be in a different position. We could set it, for instance, to step when the previous rotor had stepped 5 times. From there on, it would step every time the initial rotor was in that position.
Therefore, Enigma was a cipher where each letter was encrypted with a different simple permutation of the alphabet... but with an enormous number of possible permutations.
For a more detailed analysis of the Enigma machine, please refer to the aforementioned book, where the way the machin works is analysed, the key space size (i.e. number of possible keys) is computed and an attack is presented.