Limited Entropy Dot Com Not so random thoughts on security featured by Eloi Sanfèlix

Crypto Series: Introduction – Basic Concepts

Before getting into matter, we're gonna see the basic concepts on which great part of the text is going to relay on. Don't be scared, they are very basic :-). These are the definitions:

Cryptography is the science studying information protection, both unauthorized accesses/uses and modification of the information. Cryptography is only about using algorithms to protect this information, while Cryptanalysis is about studying techniques to break this protection, those algorithms designed by cryptographers. It's clear that both sides are intimately related, and both of them are grouped in what is known as Cryptology.

A Cryptosystem is made of the following components:

• Messages: The group of all the messages that one can encrypt. Also known as plaintext.
• Ciphertexts: The group of all encrypted messages.
• Keys: The group of all the secrets that can be used to obtain a ciphertext from a plaintext.
• Encryption and Decryption algorithms: The algorithms or transformations that need to be applied to a plaintext in order to convert it into a ciphertext or back, using a secret key.

Un Criptosistema o Sistema Criptográfico consta de los siguientes componentes:

• Mensajes: Es el conjunto de todos los mensajes que se pueden cifrar. El llamado texto en claro o plaintext.
• Criptogramas: El conjunto de todos los mensajes cifrados. En inglés llamado ciphertext.
• Claves: El conjunto de secretos que se pueden utilizar para obtener un criptograma en base a un mensaje.
• Algoritmos de cifrado y descifrado: Los algoritmos o transformaciones necesarias para convertir un mensaje en su correspondiente criptograma y viceversa, haciendo uso de una clave secreta.

So, given a cryptosystem with its encryption algorithm, which we denote as , and its corresponding decryption algorithm ( ), the following equation must hold:

Where k y k' are the corresponding encryption and decryption keys. These keys might be identical (symmetric crypto) or different (asymmetric crypto), as we'll see later.

This means that when you decrypt a message encrypted under key K using its corresponding decryption key K', you obtain the original message. Obvious, isn't it?

The figure below shows the conventional cryptosystem as depicted by C.E. Shannon in its book Communication Theory and Secrecy Systems.

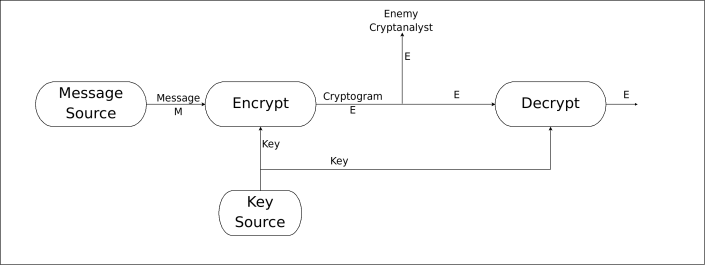
Cryptosystem scheme

Finally, to finish this post about basic concepts, we'll see how to statistically characterize a message source. Statistical characterization of a language is a quite powerful tool on its own when it's about analyzing a cipher, specially in case of basic ciphers as we'll see in the next post.

Let's imagine a message source that produces messages in a given language, for instance Spanish. We can try to characterize the source by  means of the probability that a certain character appears in the text, independent of the rest of the text.

Thus, a character c would appear with a probability . With this characterization, the word hola would appear with a probability of:

A slightly more powerful option would be characterizing the language as a series of bi-grams (i.e. groups of two characters) with a given probability. In this case, the word hello would have the following probability:

However, this option besides being an identical concept to the former one, requires of much bigger frequency tables and more effort to characterize the message source.

A question that might arise now is how would we manage to  obtain a table of relative frequencies for each one of the letters. Basically, we would take a sufficiently large text in the given language and count the number of times each letter appears. Then we divide this number by the total of letters in the text, and get its relative frequency. Frequency tables can be seen in Frequency Analysis [Wikipedia].

Next time we'll see how this frequency characterization with independent charactes can be useful to break basic ciphers.