Crypto Series: DES and AES Visualization
Thanks to previous posts in this series we already know how the DES and AES ciphers work. Now we'll use ryptool to get a better understanding of these algorithms and see how every one of the described steps works.
To this end, we first launch Cryptool and then go to Indiv. Procedures > Visualization of Algorithms > DES to see the DES algorithm. We'll get a window which will show the different steps in the algorightm, together with navigation controls that we can move somewhere else if they are placed on top of part of the animation due to our screen resolution.
This image shows one of the steps in the DES visualization:
DES Visualization
For AES we have two options. The first of them, which can be found in Indiv. Procedures > Visualization of Algorithms > AES > Rijndael animation, provides a Flash animation explaining every step in the AES cipher.
AES Visualization
The second one, accessible through Indiv. Procedures > Visualization of Algorithms > AES > Rijndael Inspector, allows us to see the AES state in every intermediate step throughout the algorithm. This would allow us to check an hypothetical AES implementation:
AES Inspector
As you can see, once again Cryptool proves itself as a valuable educational tool for Cryptography, both classical and modern algorithms.
Understanding RHUL’s SSH attack
Last week a rumor about a 0 day exploit on OpenSSH being actively exploited arose. In some places I found links to Bugtraq's note about the OpenSSH attack published in a paper of the Royal Holloway University of London back in November 2008.
The paper, Plaintext Recovery Attacks Against SSH, describes an attack which provides knowledge of 32 bits from an arbitrary ciphertext block from an SSH connection when CBC mode is used. Personally, I didn't read the paper when it was published, I just took a quick look at it and I didn't feel like reading it completely.
However, when I saw the generated stir around this issue I thought it was time to take it again. And this post is the result: an attempt to explain how the attack described in this paper works.
SSH Binary Packet Protocol
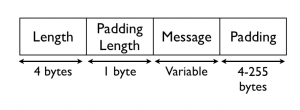
SSH BPP is the protocol in charge of defining the binary packet structure of SSH, which supports the encrypted packets that conform an SSH connection. A data packet in an SSH connection is encoded as follows:
BPP Message
The Length field ( 4 bytes) indicates the size of the remainder of the packet. The Padding length field (1 byte) encodes the length of the final padding, which makes the packet a multiple of the block size. After this field, the message is added, and finally the padding, which has to be between 4 and 255 bytes of random data.
Two cryptographic operations are applied to this message: an encryption and a MAC. The MAC is computed over a sequence number which is never transmitted (it is kept by the two ends of the communication) concatenated with the original message depicted above. The encryption is applied to the original message only.
Therefore, when SSH recieves a packet, the first thing it has to do is decrypting the first ciphertext block to obtain the message length. Then, it waits to decrypt as many bytes as the packet indicates, in order to decrypt them and check its integrity with the MAC, which provides message authentication and protects your SSH sessions against modification while they are traveling from client to server.
SSH BPP's problem
The problem with SSH BPP described in the paper is a consequence of the combination of several factors. On one side, we have that OpenSSH returns different error messages for different situations: when the decrypted length does not pass some sanity checks (e.g. it is not a multiple of the block size) and when the computed MAC does not match with the valid one. Therefore, observing the error messages one can obtain information on what caused the interruption of the connection.
On the other hand, we have that the first block indicates how many bytes the server waits for before calculating the complete MAC. Therefore, assuming the sanity checks over the message length are passed, an attacker could inject a data block, and then inject block by block until the server says "Hey, wait, the MAC does not match!".
At that point, the attacker knows that after decrypting the injected block with the server's key, the result contains in its right-most 32 bits a value equal to the number of blocks injected in the connection.
But now the complicated part starts, because the attacker needs to link these obtained 32 bits with the 32 bits that the original packet held. If the packet was encrypted with a completely unrelated key, then knowing that decrypting it under a different key gives a certain value provides basically no information on the original message.
But here CBC mode comes to play. We already know from our previous block ciphers post that this mode performs an XOR of the previous encrypted block with the current plaintext block before encrypting it with a fixed key.
Let's assume we want to obtain data from a previous packet 
But when we inject it into the connection, assuming the previous ciphertext block is known, 
So, it will decrypt the injected block, and will XOR it with the previous block. This result will be regarded as the first block of a packet, and therefore its initial 32 bits will tell the server the packet length.
Thus, we can start injecting new blocks and observing the reaction of the SSH server. Once it returns a MAC error, this means that the initial 32 bits of 
Further, from the previous two equations we can obtain the following relation:
Where the left-most 32 bits of all values at the right side of the equation are known, and the value at the left side of the equation is what we wanted to obtain. In this way we can get to know the left-most 32 bits of the target block.
Implications of this attack
So, we know how the attack works... now it's time for asking ourselves whether we should be worried about it or not. In principle, the attack is not too complex and allows the retrieval of 32 arbitrary bites of an SSH connection with a probability of 
This means that, on average, an attacker would succeed one out of 262.000 times, forcing the client to reconnect so many times to the server. I'm pretty sure anyone would be tired after 3 consecutive attemps and would think that something is wrong ;-).
Further, the attacker needs to perform a man in the middle to be able to inject data into the connection. In local area networks it's not a big deal, but over the Internet it gets more complicated.
And even then, an attacker would have 32 bits of data, 4 ASCII characters of your password... which I hope has some more than that :D. Therefore, in my opinion the attack does not have practical implications, although it's always good to update to a patched version and/or use a mode different than CBC.
What this attack actually does is contributing as an interesting example of how important details are in crypto applications and protocols. If the protocol would not depend on a length field which needs to be decrypted for waiting such a number of bytes, or would not use CBC mode or simply would not return additional information about errors (simply closing the connection indicating that something was wrong, regardless of what this something is), none of this would be possible.
Requirements for (secure) Electronic Voting
Some time ago kuasar told me about an initiative named Partido de Internet (PdI for short). The idea is to create a political party which would vote every law proposition and every initiative in the parliament depending on the results of an individual electronic election. So, affilates would vote in a per-initiative basis through the Internet, and the representatives of the PdI in the parliament would vote according to the results.
Setting aside the political implications, whether I (or you) think this is a good idea or not, I want to talk here about electronic voting. As soon as she mentioned it to me, I started thinking "Wait... this is not so easy. You know, we want elections to be secure, one doesn't want everyone to know what he voted, but he wants his vote to be counted in the right way... there are several requirements which are not so easy to meet".
So I asked her about how would they implement it... and the answer was that probably using the e-DNI, the spanish electronic id card, which of course provides digital signatures. Yeah, that's right, you could use such a device to implement an electronic voting scheme... but there is quite a lot of thinking involved in order to make it right!
Let's start here a series of posts for brainstorming about e-voting. I'll start setting up what I (and the literature I have from last year's subjects about crypto protocols 😉 ) think an electronic voting scheme needs to provide. These are the requirements I can see, but maybe you can think of some other so feel free to comment on it!
- Privacy or Anonymity: A voter wants his vote to remain anonymous. There should be absolutely no way to link a voter with its vote, neither by other voters or by the election authorities.
- Eligibility: Only voters who are eligible for voting should be able to vote, and only once. A legitimate voter should not be able to cast two different votes, and of course a non-legitimate voter should not be able to vote.
- Fariness: The results can only be obtained at the end of the elections... so that other voters cannot be influenced.
- Verifiability: The outcome of the elections needs to be fair, i.e. the results have to be equal to the votes casted by the voters.
- Individual verifiability: An individual voter can verify that his vote was actually counted.
- Receipt free: A voter cannot prove that he voted for a given party. This way one cannot be coerced to vote for a given party.
Some of these requirements are more important than others, some of them are really required for any fair electronic voting system that one can think of, and others are just desirable. In subsequent posts we will look at some electronic voting protocols and try to see which requirements they meet.
Before finishing, one thing is clear: meeting the requirements is not trivial. For instance, vote privacy and verifiability seem to pose a contradiction... how come one can only vote if he is eligible to it, but a vote cannot be revealed to anyone? We'll see some ways of doing it in some time ;-).
Crypto Series: Advanced Encryption Standard
Last time I wrote about the DES cipher, so today (yes, you guessed it) I'm writing about how the AES works. AES was created as a result of an open contest proposed by the NIST. In 1997, the NIST announced their wish to have a new encryption standard which would substitute the Data Encryption Standard and was to be called AES: Advanced Encryption Standard.
Several researchers submitted their proposals to the AES contest, but the winning candidate was the so called Rijndael cipher. This cipher was originally created by two Belgian cryptographers, Joan Daemen and Vincent Rijmen, who submitted it to the AES selection process.
The other finalists were Twofish (Bruce Schneier and others), Serpent (Ross Anderson and others), MARS (the team included Don Coppersmit) and RC6 (Ron Rivest [the R in RSA :-p ] and others).
After the contest, the NIST published AES as a FIPS standard, and since then the AES cipher has been extensively used and analyzed. In the remaining of this post we see how AES works, as we did with DES in the previous post.
NOTE: Just as in previous entry, images are taken from Wikipedia. Let me know if you try to read the post and they don't work anymore.
Crypto Series: Block Ciphers – Data Encryption Standard (DES)
The Data Encryption Standard ( DES ) was designed by IBM in 1973 as a submit for a call for proposals by the National Bureau of Standards of the United States. There was some controversy regarding to the involvement of the NSA in the development of the cipher, especially to the mysterious S-boxes and the reduced key size used, but years later it was shown that the S-boxes used where more resistant to Differential Cryptanalysis than if they had been selected at random.
The algorithm was approved as a FIPS standard in 1976, and revised up to three times in 1988,1993 and 1999. The last revision FIPS-46-3 describes the 3DES extension as a method to enlarge the key size of the DES cipher by using 3 DES operations in a row, encrypting the first time, decrypting the second time, and encrypting again the third time. This was done in order to withstand an efficient brute force attack published in 1998.
After the break (click Read more!) we'll see how it works and the main components of the algorithm.
NOTE: All images in this post are directly linked to Wikipedia. If the images are not visible anymore, let me know in the comments and I'll post my own version of the images.
Crypto Series: Block ciphers
In this entry we introduce block ciphers in a general way, as well as its modes of operation. Further, we'll see how to generate message authentication codes (MAC) using block ciphers.
Block ciphers
As we already said in the previous entry, block ciphers are symmetric ciphers which encrypt fixed length blocks. Therefore, a block cipher generally applies a series of operations combining the input block and the secret key (which isn't necessarily the same length) to obtain the output block (ciphertext).
Since they are symmetric, the decryption primitive uses the same key as the encryption primitive, and applies the operations needed to get back the plaintext at its output:
Most block ciphers can be classified as product ciphers or iterative block ciphers, based on a series of basic operations (rounds) which are repeated a number of times. These rounds provide confusion and difusion to the cipher, two concepts identified by Shannon in his famous treaty about communication theory.
Confusion refers to breaking the relationship between ciphertext and key as much as possible, while diffusion refers to destroying the statistical characteristics of the message source. Shannon identified these concepts and established the need for a secure cipher to provide them.
These kind of ciphers are generally Substitution-Permutation Networks (SPN), where several permutations (scrambling) and substitutions (changing values for others) take place one after the other, using a key, trying to achieve the goal: destroy the statistical properties of the source and obtain a secure cipher.
In subsequent entries we'll see how DES and AES, two well-known symmetric encryption standards, work. The remaining of this article treats block cipher modes of operation and how to authenticate messages using these ciphers.
Crypto Series: Introduction to modern cryptography
Let's leave aside our paper and pencil algorithms and get into modern cryptography. As most of you already know, modern cryptography is divided into two big blocks, according to the type of keys used.
On one hand, we have symmetric (key) cryptography. As you can imagine, it uses a symmetric key, shared between transmitter and receiver. This means that for each pair of entities communicating in a system, a different secret key is needed.
In this group we have block ciphers like DES/3DES and AES, as well as stream ciphers (for instance, RC4). The former divide the text into several blocks of fixed length, and encrypt block by block. The latter generally start from a key and generate a sequence of bits or bytes (key stream) from it, which will be XORed with the plaintext.
Further, there are the so-called modes of operating of block ciphers, which allow us to convert a block cipher into a stream cipher. These modes exist because for a given block cipher in its elementary mode, two identical blocks would give the same ciphertext under the same key, thus revealing part of the text structure. Later in this series we'll devote a post to these modes of operation.
However, the main problem of symmetric crypto resides in the key management. As I said, for each pair of users a secret key shared between them is needed. This means that for 3 users we would need 3 keys, for 4 users 6 keys, and in general, for n users we'd need n·(n-1)/2 keys.
As can be seen, the number of keys to be managed follows a quadratic order with the number of users to be intercommunicated. Therefore, with as few as 100 users we would need as much as 4950 different keys!
But Asymmetric or Public key Cryptography comes to help and solve this problem. This kind of cryptography works by having a key pair for each user. Each user keeps its private key secret, while its public key is known to the rest of the users ( hence the name 😉 ).
When user A wants to send a message to user B, A simply has to find B's public key, 
So far, this seems secure. Further, we just have n public keys, one per user. However, key management is still a problem: how do we make sure that a given public key pertains to a given user? In a closed environment that's easy, we just need to exchange keys in person and we're done. But... what about the Internet?
The solution is a system to determine the trust on public keys. One of the approaches is based on digital certificates, implementing what is known as a Public Key Infrastructure (PKI). Another approach is the one adoptet by PGP, based on so called trust rings. Or in other words, friends of my friends are my friends.
Finally, note that using these concepts (symmetric and asymmetric crypto), mechanisms to protect message authenticity and/or integrity can be implemented: the so called Message Authentication Codes (MAC) use symmetric crypto, while digital signatures are possible thanks to asymmetric crypto.
We'll also devote posts to all these questions in the future.
Crypto Series: Introduction to Cryptool
In this post we'll see some of the options provided by Cryptool to analyze classical ciphers, as well as using it for breaking a ciphertext encrypted with Vigenère's cryptosystem.
First step, as usual, consists of installing Cryptool. To that end, I chose using a virtual machine in VMWare with Windows XP. The installation is very simple, typical Windows app installation: Next, Next,... We'll use the English version, which is the one I have installed, but it shouldn't be difficult to follow our steps with a different version.
Once installed, this is how the main window of Cryptool looks like:
Cryptool's main window
Looking at the menus, one can see that Cryptool offers (amongst others) the possibility to encrypt and decrypt texts, cryptanalytic tools and guided tutorials. In this text we'll see how to use Cryptool for analyzing encrypted texts... Let's start with an easy one:
Gznyrém xlmlxrwz xlnl Fmrevihrwzw Klorgéxmrxz wv Ezovmxrz, l vo
Klor kziz olh znrtlh, vh fm lhxfil oftzi oovml wv vhgfwrl b kvievihróm.
Hlyivglwl, klijfv glwl zjféo ol hfurxrvmgvnvmgv olxl xlnl kziz vmgizi
vm vooz, gvmwiá jfv szxvi zotl wv ol zmgvirlinvmgv xrgzwl kziz hzori
zrilhl wv vooz. Vmgiv olh oftzivh náh xlmxfiirwlh, hv vmxfvmgizm oz
Xzhz wvo Zofnml (szyrgfzonvmgv fhzwz kziz wlinri olh qfvevh wv
nzwiftzwz, kvil gznyrém kziz qftzi z yroozi l ufgyloím, zfmjfv mlh
jfrgzm vhgv vm éklxz wv vcánvmvh), oz Yryorlgvxz (wlmwv oz tvmgv hv
wrervigv vhgfwrzmwl), b ozh krhgzh wv gvmrh b káwvo.
The text has been obtained from IEEE's cryptography challenge, by Javi Moreno and Amine Tourisa (sorry, Spanish). Actually, the solution was already published in Javi's blog, but we're gonna see how to obtain it with Cryptool:
- Create a new document ( File | New )
- Copy the text from the challenge
- Go to Analysis | Tools for Analysis | Histogram
Now we get the following frequency diagram from the text:
Frequency analysis of the ciphertext
Next we just compare this diagram with the typical one from Spanish or English, and we can see that it's simply been 'mirrored'... easy, isn't it? So the answer is, as you probably guessed, ATBASH. Decrypting the text with ATBASH (Crypt/Decrypt | Symmetric (Classic) | Substitution/Atbash ... ) , we get this cleartext (again, Spanish):
También conocida como Universidad Politécnica de Valencia, o el Poli para los amigos, es un oscuro lugar lleno de estudio y perversión. Sobretodo, porque todo aquél lo suficientemente loco como para entrar en ella, tendrá que hacer algo de lo anteriormente citado para salir airoso de ella. Entre los lugares más concurridos, se encuentran la Casa del Alumno (habitualmente usada para dormir los jueves de madrugada, pero también para jugar a billar o futbolín, aunque nos quitan este en época de exámenes), la Biblioteca (donde la gente se divierte estudiando), y las pistas de tenis y pádel.
Now we'll see how to solve a Vigenère encrypted text. Let's take as our working example the following text:
Timing attack in Google Keyczar library
Javi mailed it to me last week, and now I came across it again while reading my feeds. Nate Lawson found and described on his blog a timing (side channel) attack in Google Keyzcar library.
Take a look at his post, it's a typical problem found in string/array comparisons, and you should take it into account when programming embedded devices and any other security-related code in general.
PD: I said very soon, didn't I? 😛
Conferences, slides and documents
Yes, I know. I've been idle a looong time. I'm sorry, but I've been busy with friends and family visits, moving to a new room and other stuff. Today I bring you some links to documents of conferences, and I promise to be back very soon.
Archives Black Hat Europe 2009
Malware analysis course from F-Secure at the Helsinki University of Technology. The slides from the course are freely available for everyone.
Enjoy!