Linear Feedback Shift Registers (LFSRs)
In this post I'll provide a very simple description of linear feedback shift registers (LFSR for short). Further, we'll see how they are used to create stream ciphers. And all these things without going into mathematical details, for which I refer the interested reader to documents such as the Handbook of Applied Cryptography or this LFSR Reference.
Shift Registers
A shift register is basically a construction with interconnected several memory cells, where every cell stores one bit. So, the value of these cells conforms the so-called state of the register. When the register steps from one state to the next one (usually at each clock tick), the new state is created by simply shifting the bit in a cell to the cell next to it. Thus, the right-most bit goes out of the register, and a new bit goes into the left-most cell.
In this picture we can see an implementation of a 4 bit shift register:
Shift register
We can see an input line (Data in), 4 points where one can read the current state (Q1-Q4) and a clock input, which governs the register telling it in which moment it should step into the next state.
Linear Feedback Shift Registers (LFSRs)
Well, once you know what a shift register is, it is fairly straightforward to understand how a LFSR works. We just take the previous register and set the input as a linear combination of the different cells. Since there is a loop which feeds the register based on its previous state, we have feedback. Further, since this feedback is based on a linear function, then we have linear feedback, hence the name :).
LFSR
LFSRs' use in cryptography
So far, you probably have guessed that the main use of an LFSR in encryption systems is generating a series of pseudo-random bits to be used as a key stream in a stream cipher.
The idea is to generate a stream of bits with the minimum repetition possible, i.e. with maximal period. For its study, the connections in an LFSR are usually represented as a polynomial and the properties such a polynomial needs to meet to achieve maximal period are analyzed.
Basically, we need to get the LFSR to run through all its possible states before going back into the first one. So, if we have 16 bit registers, we'd want to have the LFSR pass through the 2^16-1 states before cycling back to the first one. And yes, I said 2^16-1 instead of 2^16 because the zero state should never appear. Otherwise the LFSR will never leave this state, since the feedback function is linear. For the curious readers, an LFSR will have maximal period if its generating polynomial is a so-called primitive polynomial (I'm pretty sure this name will ring a bell for some of you guys, although maybe not as a happy memory :P).
Setting aside the study of these polynomials, which involves somewhat comlex maths (to my non-mathematician opinion 😆 ), an LFSR by itself should not be used as a key stream generator because its properties make it fairly predictable. In fact, given an n bit LFSR, obtaining 2n bits of its output it is possible to recover the generating polynomial and be able to decrypt any subsequent text.
Therefore, LFSRs are not directly used in crypto, but they are generally used in one of these modes:
- Nonlinear combination of LFSRs: the output from several LFSRs is combined in a non-linear fashion to obtain a key stream.
- Nonlinear filter generator: the output is generated from a non-linear combination of the state.
- Clock-controlled generators: In this mode, several LFSRs step based on some rules, instead of stepping for every clock cycle.
With this kind of constructions it is possible to improve LFSR's properties for the creation of secure stream ciphers. And that's it for LFSRs from my side, for more information refer to these references:
Handbook of Applied Cryptography
Crypto Series: Introduction to stream ciphers
Today we're gonna step a little further in our Crypto series. We'll see the main properties of the so-called Stream Ciphers, how they work and some things that should be taken into account when they are used.
Later in this series, we'll see how Linear Feedback Shift Registes (LFSR) work and we'll see one of the most used stream ciphers, together with an example of wrong usage.
Keep on reading to learn more about this class of ciphers.
Crypto Series: DES and AES Visualization
Thanks to previous posts in this series we already know how the DES and AES ciphers work. Now we'll use ryptool to get a better understanding of these algorithms and see how every one of the described steps works.
To this end, we first launch Cryptool and then go to Indiv. Procedures > Visualization of Algorithms > DES to see the DES algorithm. We'll get a window which will show the different steps in the algorightm, together with navigation controls that we can move somewhere else if they are placed on top of part of the animation due to our screen resolution.
This image shows one of the steps in the DES visualization:
DES Visualization
For AES we have two options. The first of them, which can be found in Indiv. Procedures > Visualization of Algorithms > AES > Rijndael animation, provides a Flash animation explaining every step in the AES cipher.
AES Visualization
The second one, accessible through Indiv. Procedures > Visualization of Algorithms > AES > Rijndael Inspector, allows us to see the AES state in every intermediate step throughout the algorithm. This would allow us to check an hypothetical AES implementation:
AES Inspector
As you can see, once again Cryptool proves itself as a valuable educational tool for Cryptography, both classical and modern algorithms.
Crypto Series: Advanced Encryption Standard
Last time I wrote about the DES cipher, so today (yes, you guessed it) I'm writing about how the AES works. AES was created as a result of an open contest proposed by the NIST. In 1997, the NIST announced their wish to have a new encryption standard which would substitute the Data Encryption Standard and was to be called AES: Advanced Encryption Standard.
Several researchers submitted their proposals to the AES contest, but the winning candidate was the so called Rijndael cipher. This cipher was originally created by two Belgian cryptographers, Joan Daemen and Vincent Rijmen, who submitted it to the AES selection process.
The other finalists were Twofish (Bruce Schneier and others), Serpent (Ross Anderson and others), MARS (the team included Don Coppersmit) and RC6 (Ron Rivest [the R in RSA :-p ] and others).
After the contest, the NIST published AES as a FIPS standard, and since then the AES cipher has been extensively used and analyzed. In the remaining of this post we see how AES works, as we did with DES in the previous post.
NOTE: Just as in previous entry, images are taken from Wikipedia. Let me know if you try to read the post and they don't work anymore.
Crypto Series: Block Ciphers – Data Encryption Standard (DES)
The Data Encryption Standard ( DES ) was designed by IBM in 1973 as a submit for a call for proposals by the National Bureau of Standards of the United States. There was some controversy regarding to the involvement of the NSA in the development of the cipher, especially to the mysterious S-boxes and the reduced key size used, but years later it was shown that the S-boxes used where more resistant to Differential Cryptanalysis than if they had been selected at random.
The algorithm was approved as a FIPS standard in 1976, and revised up to three times in 1988,1993 and 1999. The last revision FIPS-46-3 describes the 3DES extension as a method to enlarge the key size of the DES cipher by using 3 DES operations in a row, encrypting the first time, decrypting the second time, and encrypting again the third time. This was done in order to withstand an efficient brute force attack published in 1998.
After the break (click Read more!) we'll see how it works and the main components of the algorithm.
NOTE: All images in this post are directly linked to Wikipedia. If the images are not visible anymore, let me know in the comments and I'll post my own version of the images.
Crypto Series: Block ciphers
In this entry we introduce block ciphers in a general way, as well as its modes of operation. Further, we'll see how to generate message authentication codes (MAC) using block ciphers.
Block ciphers
As we already said in the previous entry, block ciphers are symmetric ciphers which encrypt fixed length blocks. Therefore, a block cipher generally applies a series of operations combining the input block and the secret key (which isn't necessarily the same length) to obtain the output block (ciphertext).
Since they are symmetric, the decryption primitive uses the same key as the encryption primitive, and applies the operations needed to get back the plaintext at its output:
Most block ciphers can be classified as product ciphers or iterative block ciphers, based on a series of basic operations (rounds) which are repeated a number of times. These rounds provide confusion and difusion to the cipher, two concepts identified by Shannon in his famous treaty about communication theory.
Confusion refers to breaking the relationship between ciphertext and key as much as possible, while diffusion refers to destroying the statistical characteristics of the message source. Shannon identified these concepts and established the need for a secure cipher to provide them.
These kind of ciphers are generally Substitution-Permutation Networks (SPN), where several permutations (scrambling) and substitutions (changing values for others) take place one after the other, using a key, trying to achieve the goal: destroy the statistical properties of the source and obtain a secure cipher.
In subsequent entries we'll see how DES and AES, two well-known symmetric encryption standards, work. The remaining of this article treats block cipher modes of operation and how to authenticate messages using these ciphers.
Crypto Series: Introduction to modern cryptography
Let's leave aside our paper and pencil algorithms and get into modern cryptography. As most of you already know, modern cryptography is divided into two big blocks, according to the type of keys used.
On one hand, we have symmetric (key) cryptography. As you can imagine, it uses a symmetric key, shared between transmitter and receiver. This means that for each pair of entities communicating in a system, a different secret key is needed.
In this group we have block ciphers like DES/3DES and AES, as well as stream ciphers (for instance, RC4). The former divide the text into several blocks of fixed length, and encrypt block by block. The latter generally start from a key and generate a sequence of bits or bytes (key stream) from it, which will be XORed with the plaintext.
Further, there are the so-called modes of operating of block ciphers, which allow us to convert a block cipher into a stream cipher. These modes exist because for a given block cipher in its elementary mode, two identical blocks would give the same ciphertext under the same key, thus revealing part of the text structure. Later in this series we'll devote a post to these modes of operation.
However, the main problem of symmetric crypto resides in the key management. As I said, for each pair of users a secret key shared between them is needed. This means that for 3 users we would need 3 keys, for 4 users 6 keys, and in general, for n users we'd need n·(n-1)/2 keys.
As can be seen, the number of keys to be managed follows a quadratic order with the number of users to be intercommunicated. Therefore, with as few as 100 users we would need as much as 4950 different keys!
But Asymmetric or Public key Cryptography comes to help and solve this problem. This kind of cryptography works by having a key pair for each user. Each user keeps its private key secret, while its public key is known to the rest of the users ( hence the name 😉 ).
When user A wants to send a message to user B, A simply has to find B's public key, 
So far, this seems secure. Further, we just have n public keys, one per user. However, key management is still a problem: how do we make sure that a given public key pertains to a given user? In a closed environment that's easy, we just need to exchange keys in person and we're done. But... what about the Internet?
The solution is a system to determine the trust on public keys. One of the approaches is based on digital certificates, implementing what is known as a Public Key Infrastructure (PKI). Another approach is the one adoptet by PGP, based on so called trust rings. Or in other words, friends of my friends are my friends.
Finally, note that using these concepts (symmetric and asymmetric crypto), mechanisms to protect message authenticity and/or integrity can be implemented: the so called Message Authentication Codes (MAC) use symmetric crypto, while digital signatures are possible thanks to asymmetric crypto.
We'll also devote posts to all these questions in the future.
Crypto Series: Introduction to Cryptool
In this post we'll see some of the options provided by Cryptool to analyze classical ciphers, as well as using it for breaking a ciphertext encrypted with Vigenère's cryptosystem.
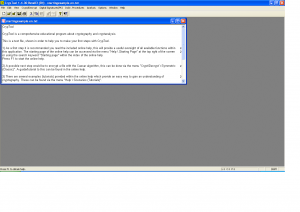
First step, as usual, consists of installing Cryptool. To that end, I chose using a virtual machine in VMWare with Windows XP. The installation is very simple, typical Windows app installation: Next, Next,... We'll use the English version, which is the one I have installed, but it shouldn't be difficult to follow our steps with a different version.
Once installed, this is how the main window of Cryptool looks like:
Cryptool's main window
Looking at the menus, one can see that Cryptool offers (amongst others) the possibility to encrypt and decrypt texts, cryptanalytic tools and guided tutorials. In this text we'll see how to use Cryptool for analyzing encrypted texts... Let's start with an easy one:
Gznyrém xlmlxrwz xlnl Fmrevihrwzw Klorgéxmrxz wv Ezovmxrz, l vo
Klor kziz olh znrtlh, vh fm lhxfil oftzi oovml wv vhgfwrl b kvievihróm.
Hlyivglwl, klijfv glwl zjféo ol hfurxrvmgvnvmgv olxl xlnl kziz vmgizi
vm vooz, gvmwiá jfv szxvi zotl wv ol zmgvirlinvmgv xrgzwl kziz hzori
zrilhl wv vooz. Vmgiv olh oftzivh náh xlmxfiirwlh, hv vmxfvmgizm oz
Xzhz wvo Zofnml (szyrgfzonvmgv fhzwz kziz wlinri olh qfvevh wv
nzwiftzwz, kvil gznyrém kziz qftzi z yroozi l ufgyloím, zfmjfv mlh
jfrgzm vhgv vm éklxz wv vcánvmvh), oz Yryorlgvxz (wlmwv oz tvmgv hv
wrervigv vhgfwrzmwl), b ozh krhgzh wv gvmrh b káwvo.
The text has been obtained from IEEE's cryptography challenge, by Javi Moreno and Amine Tourisa (sorry, Spanish). Actually, the solution was already published in Javi's blog, but we're gonna see how to obtain it with Cryptool:
- Create a new document ( File | New )
- Copy the text from the challenge
- Go to Analysis | Tools for Analysis | Histogram
Now we get the following frequency diagram from the text:
Frequency analysis of the ciphertext
Next we just compare this diagram with the typical one from Spanish or English, and we can see that it's simply been 'mirrored'... easy, isn't it? So the answer is, as you probably guessed, ATBASH. Decrypting the text with ATBASH (Crypt/Decrypt | Symmetric (Classic) | Substitution/Atbash ... ) , we get this cleartext (again, Spanish):
También conocida como Universidad Politécnica de Valencia, o el Poli para los amigos, es un oscuro lugar lleno de estudio y perversión. Sobretodo, porque todo aquél lo suficientemente loco como para entrar en ella, tendrá que hacer algo de lo anteriormente citado para salir airoso de ella. Entre los lugares más concurridos, se encuentran la Casa del Alumno (habitualmente usada para dormir los jueves de madrugada, pero también para jugar a billar o futbolín, aunque nos quitan este en época de exámenes), la Biblioteca (donde la gente se divierte estudiando), y las pistas de tenis y pádel.
Now we'll see how to solve a Vigenère encrypted text. Let's take as our working example the following text:
Crypto Series: WWII – Enigma
With this post we're leaving classical pencil and paper ciphers and getting into the mechanic ciphers used during the World War II era. We're gonna see the most famous of the cipher machins, the Enigma machine used by the Germans. Our analysis will be based on the book Applied Cryptanalysis from Mark Stamp and Richard M. Low. A very recommendable book if you are interested on cryptanalysis, really.
The Enigma Machine
The Enigma machine was developoed and patented by Arthur Scherbius in 1918, and was adopted by the nazi Germany for military and diplomacy use. Polish cryptanalysts broke the Enigma cipher in the late 1930s, and Allieds exploited this knowledge during WWII.
Máquina Enigma
It is said that thanks to Enigma being broken without the Germans noticing it (thanks to the more or less careful use of the obtained intelligence) the WWII was shortend one year or even more. There has been a lot of writing around Enigma, and I'm not an expert in the field, so I refer you to Google if you want more historical information 🙂
Encrypting and decrypting with Enigma
To encrypt with Enigma, after initializing the machine with the key as we'll see later, one simply had to press the plaintext letter to encrypt in the keyboard, and then the corresponding ciphertext letter would be enlightened in the upper (back-lighted) keyboard.
To decrypt, one had to set the machine into the corresponding state and press the received ciphertext letter. Then, in the upper keyboard the plaintext letter would get enlightened.
Enigma's features
Enigma was an electro-mechanical machine, based on the use of rotors. In the previous figure, one can easily see the mechanical keyboard and the back-lighted keyboard, which worked as input and output of the device.
Further, there is what seems to be a switchboard (stekker in German) with cables connecting one of the ends with another, and three rotors in the upper side of the machine. The configuration of these rotors and the cables of the stekker are the initial key of the machine.
Once the machine was initialized, it was possible to press in the keyboard the plaintext or ciphertext letters and obtain the ciphertext or the plaintext respectively. The workings of the machine were essantially as follows:
After pressing a key in the keyboard, a signal was sent through the corresponding stekker pin. Thanks to the cable configuration, this signal was transmitted to a different letter. Thus, the stekker worked as a mapping in the alphabet, where each letter was substituted by another one: a simple substitution.
Rotores de la máquina Enigma
After it, the signal went through the three rotors, reflected in the reflector and went back through the rotors (see figure). Finally, from the rotors it went again through the stekker, which performed a new substitution, and turned on the backlight of the corresponding letter. The net effect of the rotors and the reflector was again a permutation: each letter was converted into a different one.
However, if this were it, we would have no more than a simple substitution, with the only complexity of the use of an electromechanical machine. What Enigma added was a variation of the disposition of these rotors.
Each time a key was pressed, the rightmost rotor stepped one position. The middle rotor stepped in an odometer-like fashion, each time the rightmost rotor went through all of its steps. The leftmost rotor stepped in the same way, but depending on the middle rotor.
Further, it was possible to select the point where each rotor would step. This means that it could be when the previous rotor reached the initial position, but it could be in a different position. We could set it, for instance, to step when the previous rotor had stepped 5 times. From there on, it would step every time the initial rotor was in that position.
Therefore, Enigma was a cipher where each letter was encrypted with a different simple permutation of the alphabet... but with an enormous number of possible permutations.
For a more detailed analysis of the Enigma machine, please refer to the aforementioned book, where the way the machin works is analysed, the key space size (i.e. number of possible keys) is computed and an attack is presented.
Crypto Series: Vigenère’s Cipher (2)
As I promished, we're gonna see a different method to obtain the key length used to encrypt a text using Vigenère's algorithm. This is a method somewhat more difficult to understand than Kasiski's method, since it requires some mathematical analysis to obtain the recipe.
Friedman's test or the incidence of coincidences
This method, discovered by William F. Friedman in the 1920s, is based on computing the index of coincidences of the cryptogram's letters. The idea is that for two random letters from the cryptogram to be the same, there is a possibility that they were also the same in the original plaintext if the number of letters they have in between is a multiple of the key length.
Basically, we'll take the X first letters of the cryptogram and the X last letters, and count the number of coinciding letters in the same position. Finally, we'll divide this number by the number of letters taken and then we will have the index of coincidence.
Considering a source providing independent characters with the frequency distribution of English, and uniformly distributed characters for the key (i.e. all letters with the same frequency, 1/26 for the English alphabet), we have that:
- The probability that any two letters are the same is approximately 0.0385 when X is not a multiple of the key length
- The probability that any two letters are the same is approximately 0.0688 when X is a multiple of the key length.
So, with this process wi can determine that high values for the index of coincidence will mean that the shifted distance X is a multiple of the key length, and this way we will determine the most likely key length.
Let's see how we get these probabilities, so that we are able to obtain them in case of having a language different than English. We simply have to consider that for any two ciphertext characters 
Then, we consider two different cases: if L divides i-j, then 
![Pr[c_i=c_j] = =Pr[m_i=m_j]= sum_m Pr[m_i=m_j=m]=sum_m p(m)^2 approx 0.0688](https://s0.wp.com/latex.php?latex=Pr%5Bc_i%3Dc_j%5D+%3D+%3DPr%5Bm_i%3Dm_j%5D%3D+sum_m+Pr%5Bm_i%3Dm_j%3Dm%5D%3Dsum_m+p%28m%29%5E2+approx+0.0688&bg=ffffff&fg=000000&s=0 "Pr[c_i=c_j] = =Pr[m_i=m_j]= sum_m Pr[m_i=m_j=m]=sum_m p(m)^2 approx 0.0688")
However, when i-j is not a multiple of L, then for the two ciphertext characters to be equal the following equation needs to hold
![Pr[c_i=c_j] = Pr[ k_{j mod L} = m_i + k_{i mod L} - m_j](https://s0.wp.com/latex.php?latex=Pr%5Bc_i%3Dc_j%5D+%3D+Pr%5B+k_%7Bj+mod+L%7D+%3D+m_i+%2B+k_%7Bi+mod+L%7D+-+m_j+&bg=ffffff&fg=000000&s=0 "Pr[c_i=c_j] = Pr[ k_{j mod L} = m_i + k_{i mod L} - m_j")
But as we said before, the distribution of key characters 
![Pr[c_i=c_j] = frac{1}{26} approx 0.0385](https://s0.wp.com/latex.php?latex=Pr%5Bc_i%3Dc_j%5D+%3D+frac%7B1%7D%7B26%7D+approx+0.0385+&bg=ffffff&fg=000000&s=0 "Pr[c_i=c_j] = frac{1}{26} approx 0.0385")
That's it for today. This time there is no example, but stay tuned cause we'll see an exercise soon 🙂
And I hope next week I'm able to post some practical exercise using Cryptool to analyze a Vigenère cipher or something alike.