Limited Entropy Dot Com Not so random thoughts on security featured by Eloi Sanfèlix

Understanding RHUL’s SSH attack

Last week a rumor about a 0 day exploit on OpenSSH being actively exploited arose. In some places I found links to Bugtraq's note about the OpenSSH attack published in a paper of the Royal Holloway University of London back in November 2008.

The paper, Plaintext Recovery Attacks Against SSH, describes an attack which provides knowledge of 32 bits from an arbitrary ciphertext block from an SSH connection when CBC mode is used. Personally, I didn't read the paper when it was published, I just took a quick look at it and I didn't feel like reading it completely.

However, when I saw the generated stir around this issue I thought it was time to take it again. And this post is the result: an attempt to explain how the attack described in this paper works.

SSH Binary Packet Protocol

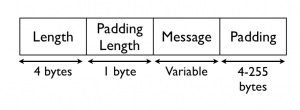
SSH BPP is the protocol in charge of defining the binary packet structure of SSH, which supports the encrypted packets that conform an SSH connection. A data packet in an SSH connection is encoded as follows:

BPP Message

The Length field ( 4 bytes) indicates the size of the remainder of the packet. The Padding length field (1 byte) encodes the length of the final padding, which makes the packet a multiple of the block size. After this field, the message is added, and finally the padding, which has to be between 4 and 255 bytes of random data.

Two cryptographic operations are applied to this message: an encryption and a MAC. The MAC is computed over a sequence number which is never transmitted (it is kept by the two ends of the communication) concatenated with the original message depicted above. The encryption is applied to the original message only.

Therefore, when SSH recieves a packet, the first thing it has to do is decrypting the first ciphertext block to obtain the message length. Then, it waits to decrypt as many bytes as the packet indicates, in order to decrypt them and check its integrity with the MAC, which provides message authentication and protects your SSH sessions against modification while they are traveling from client to server.

SSH BPP's problem

The problem with SSH BPP described in the paper is a consequence of the combination of several factors. On one side, we have that OpenSSH returns different error messages for different situations: when the decrypted length does not pass some sanity checks (e.g. it is not a multiple of the block size) and when the computed MAC does not match with the valid one. Therefore, observing the error messages one can obtain information on what caused the interruption of the connection.

On the other hand, we have that the first block indicates how many bytes the server waits for before calculating the complete MAC. Therefore, assuming the sanity checks over the message length are passed, an attacker could inject a data block, and then inject block by block until the server says "Hey, wait, the MAC does not match!".

At that point, the attacker knows that after decrypting the injected block with the server's key, the result contains in its right-most 32 bits a value equal to the number of blocks injected in the connection.

But now the complicated part starts, because the attacker needs to link these obtained 32 bits with the 32 bits that the original packet held. If the packet was encrypted with a completely unrelated key, then knowing that decrypting it under a different key gives a certain value provides basically no information on the original message.

But here CBC mode comes to play. We already know from our previous block ciphers post that this mode performs an XOR of the previous encrypted block with the current plaintext block before encrypting it with a fixed key.

Let's assume we want to obtain data from a previous packet , which is part of the current SSH connection. After decrypting it we would have:

But when we inject it into the connection, assuming the previous ciphertext block is known, , then the SSH server will compute this:

So, it will decrypt the injected block, and will XOR it with the previous block. This result will be regarded as the first block of a packet, and therefore its initial 32 bits will tell the server the packet length.

Thus, we can start injecting new blocks and observing the reaction of the SSH server. Once it returns a MAC error, this means that the initial 32 bits of contain the number of bytes we injected so far.

Further, from the previous two equations we can obtain the following relation:

Where the left-most 32 bits of all values at the right side of the equation are known, and the value at the left side of the equation is what we wanted to obtain. In this way we can get to know the left-most 32 bits of the target block.

Implications of this attack

So, we know how the attack works... now it's time for asking ourselves whether we should be worried about it or not. In principle, the attack is not too complex and allows the retrieval of 32 arbitrary bites of an SSH connection with a probability of . This probability comes from the conditions that need to be satisfied in order to pass the sanity checks after decrypting the injected block.

This means that, on average, an attacker would succeed one out of 262.000 times, forcing the client to reconnect so many times to the server. I'm pretty sure anyone would be tired after 3 consecutive attemps and would think that something is wrong ;-).

Further, the attacker needs to perform a man in the middle to be able to inject data into the connection. In local area networks it's not a big deal, but over the Internet it gets more complicated.

And even then, an attacker would have 32 bits of data, 4 ASCII characters of your password... which I hope has some more than that :D. Therefore, in my opinion the attack does not have practical implications, although it's always good to update to a patched version and/or use a mode different than CBC.

What this attack actually does is contributing as an interesting example of how important details are in crypto applications and protocols. If the protocol would not depend on a length field which needs to be decrypted for waiting such a number of bytes, or would not use CBC mode or simply would not return additional information about errors (simply closing the connection indicating that something was wrong, regardless of what this something is), none of this would be possible.