Crypto Series: Vigenère Cipher
Today we're gonna go a little further on the study of classical ciphers. We're gonna see an evolution of simple substitution ciphers known as Vigenère cipher, how it works and cryptanalysis methods that we can apply.
Vigènere Cipher
This cipher is named after the Frenchman Blaise de Vigènere, to whom it was wrongly attributed in the 19th century. Actually it's a quite simple cipher combining several Caesar's ciphers according to a secret key. An example will help to understand it.
If the key is abcs, then the first letter is encrypted shifting it 0 times, second letter 1 time, third letter 2 times, fourth letter 3 times, and then we start again with 0 times. So, the key is repeated as many times as needed to encrypt the complete plaintext. This operation can be seen as a two entries subtitution table (tabula recta or Vigenère's table):
Vigènere table
Using this table, the row corresponds to the plaintext letter to encrypt and the column corresponding to the key letter will give us the resulting cryptogram letter. To decrypt, we should place ourselves in the row corresponding to the key letter, move right up to the cryptogram's letter column, and then move upwards to know which plaintext letter corresponds looking at the column header.
Let's take a look at an example.We want to encrypt the word WADALBERTIA with the key ERP, so we write down the letter with the key below, repeated as many times as needed to reach the word's number of characters:
WADALBERTIA
ERPERPERPER
In order to obtain our result using the table, we go to column W and go down till row E. This gives us our first cryptogram letter, A. Then we repeat the operation with column A and row R, which brings us R. We repeat this process with the remaining letters and finally obtain ARSECQIIIMR.
For decryption, we would go to the key's letter, for instance E. Then we would move right through the columns to find an A, and then we would move up to the header to see that this is encrypted labeled as letter W. Continuing until the end, we would get back our input plaintext.
Attacking Vigenère's cipher
Now that we know how it works, we can proceed to see how we could break this cipher. It's clear that the simple method applied to Caesar's cipher is not useful here, since each letter is encrypted independently of the previous one. However, if we have a key of length L, every L letters the sequence is repeated. Thus, we have L different Caesar's ciphers and we could break them as we learnt last time.
To do so, we need to determine L. Therefore, Vigenère's cipher cryptanalisis will focus on methods to find out how long is the key, so that we can analyse later on the different Caesar ciphers. We will study two different methods to obtain it.
Kasiski's method
This method is based on looking for repeated patterns in the cryptogram. Kasiski observed that for a given pair of repeated fragments in the plaintext to be encrypted two times in the same way, the distance between them must be a multiple of the key length. Then, each letter of the repeated string will be encrypted with the same part of the key. Let's see an example taken from Wikipedia:
abcdeabcdeabcdeabcdeabcdeabcdeabc crypto is short for cryptography.
In this case, we can see that the string crypt would be encrypted both times by abcde. This is due to the fact that the key is 5 characters long (abcde) and the distance between the two appearances of crypto is 20 characters ( 4 times 5). In case the distance was not a multiple of 5, this wouldn't occur.
Therefore, in this case we could sey that the key length should be one of the divisors of 20: 1,2,4,10 and 20. However, if we encounter any other repetition, then we can reduce the search space to the common divisors of both distances. With several repetitions, it could be possible to reduce the number of candidates to one and therefore discover the key length.
Obviously, it might be that some of the repetitions are just coincidence. Thus, it is possible that the different distances have a greatest common divisor of 1, which means that they only have 1 as a common divisor. This would lead us to discard some of the repetitions found; but following this method we would be able to reduce the key length to a very few candidates. Then all what is needed is to analyze the different Caesar's ciphers that form the Vigènere cipher.
Next post
We're gonna stop here for now, cause I've had the post half-way written for two weeks and didn't have time to finish it... Next time we'll revisit Vigenère's cipher with another method to obtain the key length and some examples.
I hope you're enjoying it 🙂
Crypto Series: Classical ciphers
During some posts we're gonna get introduced into classical ciphers. From Wikipedia, "a classical cipher is a type of cipher used historically but which now have fallen, for the most part, into disuse".
This post will study one of the most known classical ciphers, the Caesar cipher, and other similar ciphers.
Caesar Cipher
Caesar's cipher, named after Julius Caesar, is a substitution cipher that simply substitutes each letter by the letter K positions to the right in the alphabet. So, for a K value of 3, A would be encrypted as D, B as E, C as F and so on.
In mathematical terms, considering an alphabet with 26 letters, where A would be letter 0 and Z letter 25, we can define these encryption and decryption operations as:
Where 
As you can see, very simple. For instance, if we encrypt the sentence CRIPTOGRAFIA PARA TODOS under key 5, we get the following ciphertext: HWNUYTLWFKNF UFWF YTITX.
Here we can already see one of the weaknesses of this cipher: the structure of the plaintext remains. As you can see, last word in the message starts with a Y, then it has two T's, one I and one X. Therefore, we know that this word has the second and fourth letter identical. Also second and fourth letters are identical in the second word, but different to the ones in the last word.
This, in a large text and within a context, could lead us to decipher great part of the text. For instance, knowing that it's a text about information security, we can try to find words with the same structure as security or information and map these letters for all the text. With this, we would have parts of other words, and with some luck we would be able to obtain more letters by guessing those words. Continuing like this, at the end we would have the complete text.
Another tool that allows us to easily analyse this kind of ciphers is frequency analysis, which we mentioned previously. If we take a text encrypted using this system and count the number of appearances of each letter, and then obtain (or generate) a table of relative frequencies for the target language, we can match the most frequent letter in the ciphertext and the most frequent letter in the target language.
Then, since the same shift is applied to all the letters, we would have the key and would be able to obtain the complete message. In case of getting a non-sense message, we could try with the second most frequent letter instead of the first one. Since it's a statistical analysis, it's possible that the character distribution in our text doesn't completely match the original distribution, but will certainly be similar.
Simple substitution ciphers
Caesar's cipher we just analysed is one of the so-called simple substitution ciphers, which always substitute each symbol of the input alphabet by a given symbol of the output alphabet.Besides Caesar's cipher, Atbash cipher is another quite famous substitution cipher, where each the alphabet is inverted: A->Z, B->Y, ... Y->B, Z->A.
But not only these two simple substitution ciphers exist. We can create any modification of the input alphabet as output alphabet. Even then, all these ciphers suffer from the same problem: the structure is maintained and they are quite easy to break using frequency analysis and word matching.
Example: Breaking a simple substitution cipher
This time I encrypted an English text. This is how the ciphertext looks like:
ZL VAGRERFGF NOBHG FRPHEVGL ERYNGRQ GBCVPF UNIR QEVSGRQ N YVGGYR OVG, ZBIVAT SEBZ CHER FBSGJNER NAQ ARGJBEXVAT FRPHEVGL GB PELCGBTENCUL NAQ CENPGVPNY NGGNPXF BA PELCGBTENCUVP VZCYRZRAGNGVBAF, YVXR FVQR PUNAARY NANYLFVF NGGNPXF.
VA GUVF EROBEA OYBT V JVYY GEL GB VAGEBQHPR GUR ERNQREF VAGB GURFR GBCVPF JVGUBHG TRGGVAT VAGB GBB PBZCYRK ZNGUF. GUR NVZ VF GB CEBIVQR NA HAQREFGNAQVAT BS PELCGBTENCUL JVGUBHG UNIVAT ERNQREF YBFG BA ZNGURZNGVPNY PBAPRCGF. LBH JVYY GRYY JURGURE V NPUVRIR GUVF TBNY BE ABG.
Looks pretty complicated, doesn't it? Let's see how to approach this example, assuming this is a simple substitution cipher. First of all, we're gonna count how many times appears each letter, and then divide it by the total number of letters. I've done it with this simple program I quickly coded, although it's possible to do it with Cryptool but I don't have it available right now.
Once it's done, we sort it by frequency. For instance, copy-pasting the output of the program into a spreadsheet in Google Docs and pressing order by the corresponding column. The top 3 letters are:
G 52 0.124402
R 38 0.090909
V 37 0.088517
So, we go to a frequency table for English (here) and see that E is the most frequent letter in this language. Now we subtract 'G'-'E'=7. If we apply this key using a Caesar's cipher, we just get garbage. However, if we take 'R' as 'E, then 'R'-'E'=13. Deciphering using Caesar's cipher, we get:
MY INTERESTS ABOUT SECURITY RELATED TOPICS HAVE DRIFTED A LITTLE BIT, MOVING FROM PURE SOFTWARE AND NETWORKING SECURITY TO CRYPTOGRAPHY AND PRACTICAL ATTACKS ON CRYPTOGRAPHIC IMPLEMENTATIONS, LIKE SIDE CHANNEL ANALYSIS ATTACKS.
IN THIS REBORN BLOG I WILL TRY TO INTRODUCE THE READERS INTO THESE TOPICS WITHOUT GETTING INTO TOO COMPLEX MATHS. THE AIM IS TO PROVIDE AN UNDERSTANDING OF CRYPTOGRAPHY WITHOUT HAVING READERS LOST ON MATHEMATICAL CONCEPTS. YOU WILL TELL WHETHER I ACHIEVE THIS GOAL OR NOT.
Much more readable 🙂 Don't you recognize it? Look at http://www.limited-entropy.com/en/about 🙂
We've decrypted the text, although not at our first try, but at our second. Another option would have been using 'G' as 'T', since T is the second most frequent letter in English. The result is exactly the same.
However, facing an unknown transformation, we would have been to play with other hints besides frequency analysis. For instance, we could use the fact that we expected to see CRYPTOGRAPHY in the text, and assign this word to the only word in the ciphertext that has the same letter in the third and the last position. Then, we would substitute all its letters in the ciphertext and would see if it makes any sense.
From there, we just need to continue on guessing letters... kind of a puzzle 🙂
That's it for today, I hope you're liking it :). Questions and comments are more than welcome!
Crypto Series: Classification of Attacks
As a quick note on the cryptographic systems description on the previous post, I'd like to mention that atacks to cryptosystems are usually classified based on the information known to the cryptanalyst. The basic types of attacks are:ásicos son:
- Ciphertext-only: The cryptanalyst knows only the ciphertext, and often also some information about the context of the message.
- Known-Plaintext: The cryptanalyst knows pairs of plaintexts and corresponding ciphertexts.
- Chosen-Plaintext: The cryptanalyst is able to choose plain texts and obtain their corresponding ciphertexts.
- Chosen-Ciphertext: The cryptanalyst can choose any ciphertext and obtain its corresponding plaintext.
Although the final two kinds could seem to be identical, there is a big difference mainly when applied to public key algorithms. In these algorithms, it is usually very easy to encrypt any plaintext. Thus, these algorithms need to withstand chosen-plaintext attacks. However, a chosen-ciphertext attack would require a decryption oracle, which would return any ciphertext decrypted without exposing the decryption key.
Crypto Series: Introduction – Basic Concepts
Before getting into matter, we're gonna see the basic concepts on which great part of the text is going to relay on. Don't be scared, they are very basic :-). These are the definitions:
Cryptography is the science studying information protection, both unauthorized accesses/uses and modification of the information. Cryptography is only about using algorithms to protect this information, while Cryptanalysis is about studying techniques to break this protection, those algorithms designed by cryptographers. It's clear that both sides are intimately related, and both of them are grouped in what is known as Cryptology.
A Cryptosystem is made of the following components:
- Messages: The group of all the messages that one can encrypt. Also known as plaintext.
- Ciphertexts: The group of all encrypted messages.
- Keys: The group of all the secrets that can be used to obtain a ciphertext from a plaintext.
- Encryption and Decryption algorithms: The algorithms or transformations that need to be applied to a plaintext in order to convert it into a ciphertext or back, using a secret key.
Un Criptosistema o Sistema Criptográfico consta de los siguientes componentes:
- Mensajes: Es el conjunto de todos los mensajes que se pueden cifrar. El llamado texto en claro o plaintext.
- Criptogramas: El conjunto de todos los mensajes cifrados. En inglés llamado ciphertext.
- Claves: El conjunto de secretos que se pueden utilizar para obtener un criptograma en base a un mensaje.
- Algoritmos de cifrado y descifrado: Los algoritmos o transformaciones necesarias para convertir un mensaje en su correspondiente criptograma y viceversa, haciendo uso de una clave secreta.
So, given a cryptosystem with its encryption algorithm, which we denote as 
Where k y k' are the corresponding encryption and decryption keys. These keys might be identical (symmetric crypto) or different (asymmetric crypto), as we'll see later.
This means that when you decrypt a message encrypted under key K using its corresponding decryption key K', you obtain the original message. Obvious, isn't it?
The figure below shows the conventional cryptosystem as depicted by C.E. Shannon in its book Communication Theory and Secrecy Systems.
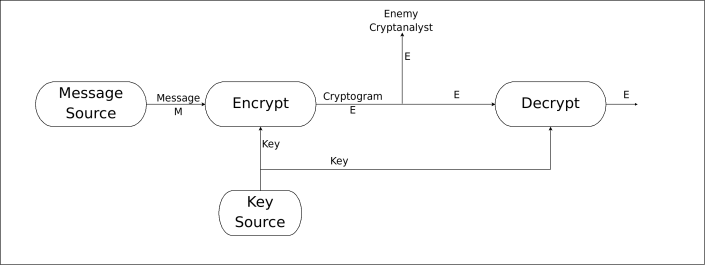
Cryptosystem scheme
Finally, to finish this post about basic concepts, we'll see how to statistically characterize a message source. Statistical characterization of a language is a quite powerful tool on its own when it's about analyzing a cipher, specially in case of basic ciphers as we'll see in the next post.
Let's imagine a message source that produces messages in a given language, for instance Spanish. We can try to characterize the source by means of the probability that a certain character appears in the text, independent of the rest of the text.
Thus, a character c would appear with a probability 
A slightly more powerful option would be characterizing the language as a series of bi-grams (i.e. groups of two characters) with a given probability. In this case, the word hello would have the following probability:
However, this option besides being an identical concept to the former one, requires of much bigger frequency tables and more effort to characterize the message source.
A question that might arise now is how would we manage to obtain a table of relative frequencies for each one of the letters. Basically, we would take a sufficiently large text in the given language and count the number of times each letter appears. Then we divide this number by the total of letters in the text, and get its relative frequency. Frequency tables can be seen in Frequency Analysis [Wikipedia].
Next time we'll see how this frequency characterization with independent charactes can be useful to break basic ciphers.
Crypto series: Planning
With this post we start with a series about cryptography, which I hope catches your attention. The series is divided into several chapters, with the following (very rough) planning:
- Introduction
- Symmetric Cryptography
- Asymmetric Cryptography
- Hash functions and authentication codes
- Cryptographic protocols
- Cryptographic Systems
Each chapter will be made of several theory posts and one or various practice posts, which we'll do using tools like Cryptool. To easily identify these posts, although they'll most likely be pretty much all my posts, I'll name them this way: Crypto: Chapter/Section.
I'll start very shortly with the first chapter, Introduction, where we'll see basic concepts and classical crypto amongst other things.
Any feedback as of now?